Next: Example Up: Basic theory Previous: Predictive densities
The range of problems for which an analytic solution is possible is limited and depends on the choice of the model (leading to a tractable likelihood function) and prior.
A simple model assumes that the data
![]() is
a random sample, of size
is
a random sample, of size ![]() , from some distribution having density
function
, from some distribution having density
function
![]() with
with
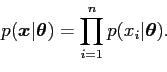 |
(11) |
If a prior
![]() is chosen from some family
is chosen from some family
![]() , say
, say
![]() , the choice of
, the choice of
![]() being
regarded as part of the model specification, the posterior is given by
being
regarded as part of the model specification, the posterior is given by
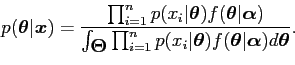 |
(12) |
If
![]() is also a member of
is also a member of ![]() , say
, say
| (13) |
where the parameter
![]() is a function of only
is a function of only
![]() and
and
![]() then the family
then the family ![]() is said to be closed
under sampling, with respect to the density
is said to be closed
under sampling, with respect to the density
![]() , (Barnard, 1949). The prior
, (Barnard, 1949). The prior
![]() is called a
conjugate prior for
is called a
conjugate prior for
![]() (see Smith and Bernardo, 1994, p. 265).
(see Smith and Bernardo, 1994, p. 265).