Numerical approach

The interest is in what may be inferred about ${\mbox{\boldmath$\theta$}} = (\mu)$ from a random sample ${\mbox{\boldmath$x$}} = (x_1, x_2, \ldots , x_n)^T$. Each component of the random sample is modeled as a value of $X$, being independently and identically distributed as $N(\mu, \sigma^2)$. Hence the probability density function (pdf) for the whole sample, the likelihood function, can be written as

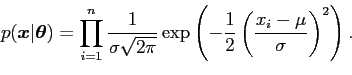$$p({\mbox{\boldmath$x$}} \vert {\mbox{\boldmath$\theta$}}) =... ...eft(-\frac{1}{2}\left(\frac{x_i-\mu}{\sigma}\right)^2\right).$$ (39)

The prior is as given above, which may, in practice, be a setting up value $(\mu)$ and a measure of variation derived from system history $(\sigma^2)$.

It is possible to numerically apply Bayes' Theorem. Of the many approaches to numerically applying Bayes' Theorem, Bayes4 a suite of software developed by Dr J C Naylor (see Naylor, 1982), Naylor and Shaw (1983) and Naylor and Smith (1982)) is chosen here. Bayes4 uses Gauss-Hermite quadrature to obtain values for posterior density parameters. Applying Bayes4 gives the posterior densities shown in figure 4 and also a numerical approximation to the posterior mean for $\mu$ of $3.508$.

Figure:Posterior mean and predictive density, Normal prior.

Repeating the exercise using a Student's t-distribution with 4 degrees of freedom ($t_{\nu =4}$) as prior, renders the calculation analytically intractable. However, using Bayes4 gives the posterior densities shown in figure 5, where the posterior estimate for $\mu$ is again $3.508$.

Figure:Posterior mean and predictive density, $t_{\nu =4}$ prior.

All of the examples above are extremely easy to describe. However, as soon as a $t_{\nu =4}$ prior is chosen their solution becomes, analytically at least, intractable. At the same time the result of the analysis is remarkably similar to that obtained with a Normal prior. Performing the analysis using Bayes4 is no more difficult than when a Normal prior is used.

The graphs in figure 4,5 were produced using standard S-Plus routines, which apply spline curves, to interpolate between points.

The problem analysed in the preceding sections is univariate and simple; the use of these methods is complete overkill but is done for comparison. In each case the posterior means and the predictive densities are the same, as is the inference to be drawn from the data. If the problem exceeds 3 parameters, the methods of generating the posterior samples are still valid, as long as they can be applied to the problem. However, the display techniques used are not available for exploring the results derived from them. A uniform way of presenting results from higher dimensional objects would be useful.