Next: Simulation approach Up: Implementation Example Previous: Implementation Example
The interest is in inference about
![]() given
given
![]() .
.
With prior
![]()
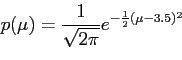 |
(24) |
![]() , the sample mean, is a sufficient statistic for
, the sample mean, is a sufficient statistic for ![]() , as
the likelihood,
, as
the likelihood,
![]() , depends only on
, depends only on
![]() and
and
![]() (fixed), through the sampling distribution of
(fixed), through the sampling distribution of ![]() which is
which is
![]()
| (25) | |||
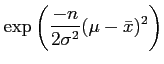 |
(26) |
so the posterior for ![]() is
is
| (27) | |||
| (28) |
So, by inspection
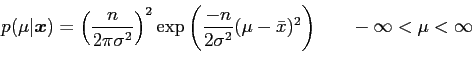 |
(29) |
![]() is a random sample of size
is a random sample of size ![]() from
from
![]() where
where ![]() is known and the prior for
is known and the prior for ![]() is
is
![]() . The posterior is
. The posterior is
![]() where
where
 |
(30) |
and
| (31) |
The prior for ![]() is
is ![]() ,
, ![]() and
and
![]() so
posterior belief about
so
posterior belief about ![]() is as if
is as if ![]() had a
had a
![]() distribution.
distribution.
danny 2009-07-23