Simulation approach

It is possible to utilise Monte Carlo integration using Markov Chains (MCMC) to obtain inference about population statistics in many problems. An MCMC solution to a problem consists of an MCMC constructed so that its stationary distribution is the distribution about which it is wished to draw inference, (see, for example, Gilks et al., 1996). The problem outlined in section 2 is amenable to this approach. Specifics of the method used are discussed in .

As a simple example of the use of MCMC to solve the above problem choose a Metropolis-Hastings, random walk MCMC. This has the advantage of allowing the use of a symmetrical distribution from which to choose the candidate.⁴ Once the process has entered the state space of the target distribution⁵ it will not leave it.

Here

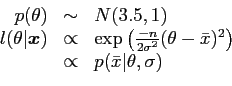$$\begin{array}{rcl} p(\theta) & \sim & N(3.5, 1) \\ l(\th... ... & \propto & p(\bar x \vert \theta, \sigma) \\ \end{array}$$ (32)

so the probability of transition from $\theta_1$ the current state to $\theta_2$ the candidate state is

$$\begin{array}{rcl} p(\theta_1, \theta_2) & = & \min \left(... ..._1)p(\bar x\vert\theta_1, \sigma)} , 1 \right) \end{array}$$ (33)

The code shown in figure 2 is for running a Metropolis-Hastings, random walk MCMC sampler. With the transition probability above, and allowing 1000 samples as a burn in period, the output is a sample of 1000 values with $\hat \mu = 3.507999$ and ${\mbox{sd }}= 0.00304$. (Note that this result would, of course, be slightly different if run again, due to the small sample used and random differences. However, if a large enough sample is taken, run differences tend to zero with probability $1$).

It is possible to draw a predictive sample from this density with the S-Plus command y$\leftarrow$rnorm(1000, samp, 0.01)⁶, where samp is the output from the sampler, this gives the histogram shown in figure 1.

Figure:Histogram of predictive sample of 1000 drawn from the density $\mu$ $N(3.507999, 0.00304^2)$.

1

Figure:S Plus code for the MCMC example.

1.5