Discussion
- The Bayes Density Estimator provides a kernel density estimate, without
the need for bandwidth choice by the user. This has the distinct advantage
that, when applied to a series of projections, the bandwidth need not be
assumed to be the same for all projections. The corollary to this is that the
data need not be distorted in trying to ensure uniform smoothness for all
projections.
- The model found by the BKDE should be the
best available from the family of models provided (Berk, 1966), which, in
the case of KDE
models, gives a wide range to choose from. This leads to a high degree of
confidence in the density estimate obtained.
- The bandwidth found is not a point estimate but a density with location
and shape parameters. This allows for examination of the chosen bandwidth for
suitability and might lead, in further work, to a system of kernel suitability
evaluation.
- The choice of kernel affects the final model, some kernels
being more suitable for particular types of data, for example, survival data is
not well served by any kernel that allows negative values. The BKDE allows for
rapid selection of kernel and might lead to suitability analysis of the kernel.
- The prior allows for the modelling of belief in the smoothness of the
underlying density. The strength of that belief can also be represented and
allows for a wide variation in the balance between that belief and the
information from the data.
- With the large samples obtained from MCMC simulation, the prior is
dominated by the information from the data in the likelihood, however it is
possible to force a ``wrong'' prior on the system. A very strongly held belief
in a prior, for example
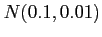 in section 2 needs
significantly more data to modify than that of
in section 2 needs
significantly more data to modify than that of 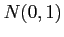 . used in graph 1. of
Figure 2.
. used in graph 1. of
Figure 2.
The examples from Berlinet and Devroye (1994) are designed to be difficult and the results
in that paper are all averages of 20 different samples of size 100. The
overwhelming conclusion to be drawn from it is that no one KDE will do well at
all densities and some experimentation with method is needed. However, the BKDE
in one of its forms produced acceptable estimates of a large number of the
densities without the need for human intervention. As a method KDE compares
well to several others and can be considered at least the equal of most.
danny
2009-07-23