Example

As an illustration, consider inference about the mean $\theta$ of an exponential distribution with density

$$p(x\vert\theta) = \theta^{-1} e^{-x/\theta}      (x > 0, \theta > 0).$$ (14)

The likelihood of a random sample ${\mbox{\boldmath$x$}} = (x_1, x_2, \ldots , x_n)^T$ is

$$p({\mbox{\boldmath$x$}} \vert \theta) = \theta^{-n} e^{-n \bar x/\theta}$$ (15)

in terms of the sufficient statistic³

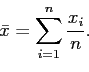$$\bar x = \sum_{i=1}^n \frac{x_i}{n}.$$ (16)

Take as prior a density of the form

$$p(\theta) = f(\theta \vert \alpha_1, \alpha_2)$$ (17)

$$= \frac{\alpha_2^{\alpha_1-1}}{\Gamma(\alpha_1-1)} \theta^{-\alpha_1} e^{-\alpha_2/\theta}$$ (18)

$$\propto \theta^{-\alpha_1} e^{-\alpha_2/\theta}$$ (19)

then the corresponding posterior is

$$p(\theta\vert{\mbox{\boldmath$x$}}) \propto \theta^{-\alpha_1}e^{-\alpha_2/\theta} \theta^{-n} e^{-n\bar x / \theta}$$ (20)

$$= \theta^{-(\alpha_1 + n)} e^{-(\alpha_2 +n\bar x)/\theta}$$ (21)

which is clearly also of the form (17) and so may be written as

$$p(\theta\vert{\mbox{\boldmath$x$}}) = f(\theta \vert \alpha_1^\prime, \alpha_2^\prime)$$ (22)

where

$$\alpha_1^\prime = \alpha_1 + n\mbox{ , and } \alpha_2^\prime = \alpha_2 + n\bar x$$ (23)

Hence (14) is closed under sampling, with (17) as a convenient natural conjugate prior family for inference about the mean $\theta$. In such a case a complete analytic solution is available.